Five Number Summary

Five Number Summary Calculator

Enter your dataset below to instantly compute the five number summary (minimum, Q1, median, Q3, and maximum). helping you analyze your data quickly and accurately. Supports comma, space, or semicolon separated values.

How the Five Number Summary is Calculated

What is the Five Number Summary?

The five number summary is a statistical method that provides a quick overview of your data distribution using just five key values: minimum, first quartile (Q1), median (Q2), third quartile (Q3), and maximum.

This powerful tool helps you understand the center, spread, and shape of your data without being affected by extreme outliers.

When to Use It

  • • Exploratory data analysis
  • • Comparing multiple datasets
  • • Identifying outliers
  • • Understanding data distribution
  • • Creating box plots

Step-by-Step Calculation Process

Step 1: Data Preparation

Ensure your data consists of numerical values (integers or decimals) separated by commas, spaces, or semicolons. The calculator automatically cleans and validates your input.

Step 2: Data Sorting

Your data is automatically sorted in ascending order (from smallest to largest) to prepare for calculation.

Step 3: Calculate Core Values

Minimum & Maximum

The smallest and largest values in your dataset.

Median (Q2)

The middle value that divides your data into two equal halves.

First Quartile (Q1)

The median of the lower half of your data.

Third Quartile (Q3)

The median of the upper half of your data.

Step 4: Special Cases

For datasets with only 3 values, Q1 equals the minimum and Q3 equals the maximum, ensuring meaningful results even with limited data.

Understanding Your Results

What Each Value Tells You

  • Minimum: The lowest value in your dataset
  • Q1: 25% of your data falls below this value
  • Median: The center of your data distribution
  • Q3: 75% of your data falls below this value
  • Maximum: The highest value in your dataset

Key Insights

  • • Range: Maximum - Minimum shows data spread
  • • IQR: Q3 - Q1 shows middle 50% spread
  • • Skewness: Compare median position to detect asymmetry
  • • Outliers: Values beyond 1.5 × IQR from Q1/Q3

Examples

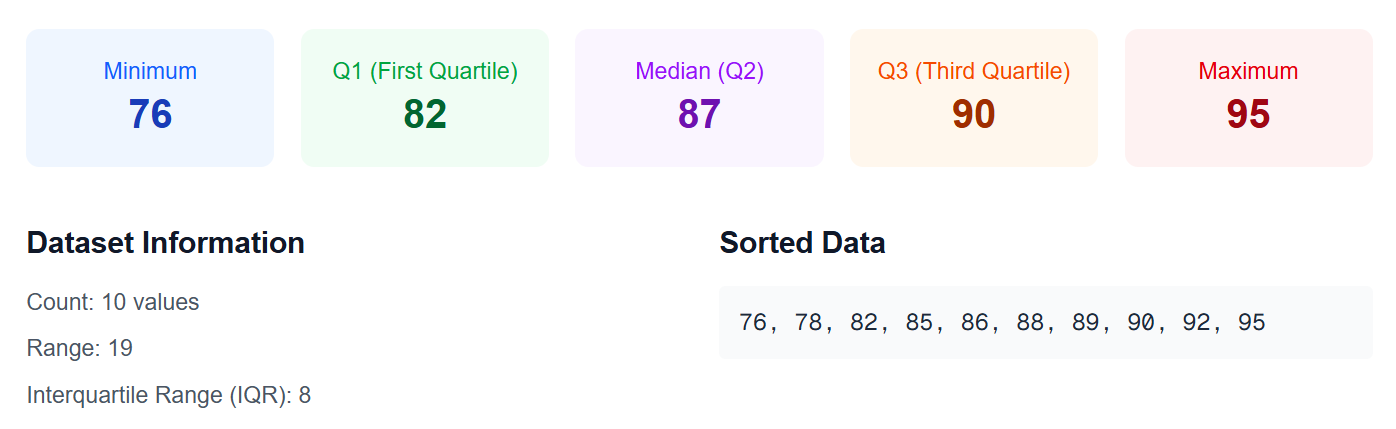
Dataset 1: Student Test Scores

78, 85, 90, 92, 88, 76, 95, 89, 82, 86
  • Minimum: 76
  • Q1: 82
  • Median (Q2): 87
  • Q3: 90
  • Maximum: 95
Most scores are between 80 and 90, with no significant outliers.
Five number summary box plot for student test scores

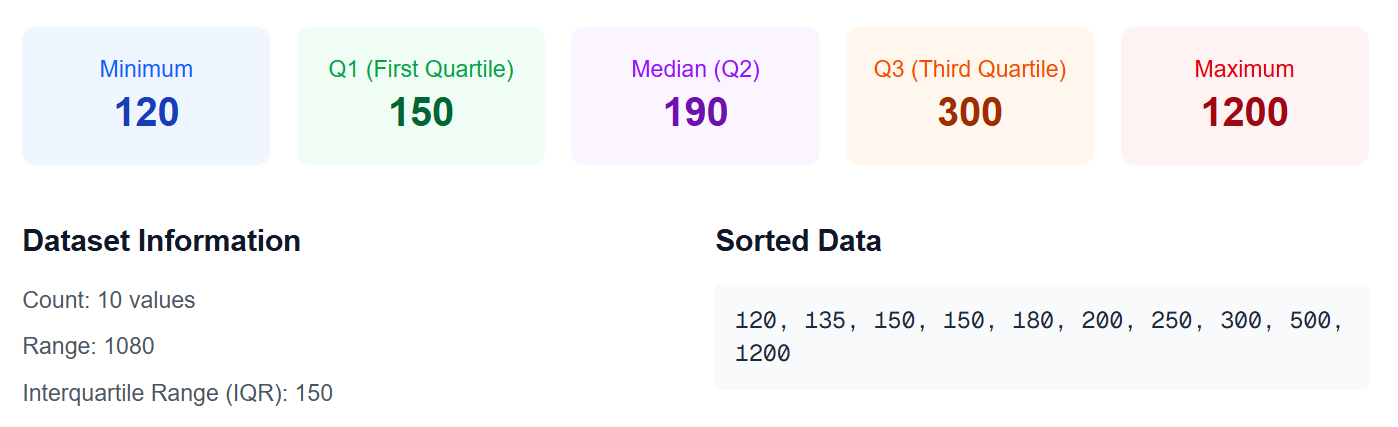
Dataset 2: E-commerce Order Amounts

120, 150, 180, 200, 250, 300, 500, 1200, 150, 135
  • Minimum: 120
  • Q1: 150
  • Median (Q2): 190
  • Q3: 300
  • Maximum: 1200
Most orders are under $300, but there is a high-value order ($1200) as an outlier.
Five number summary box plot for e-commerce order amounts

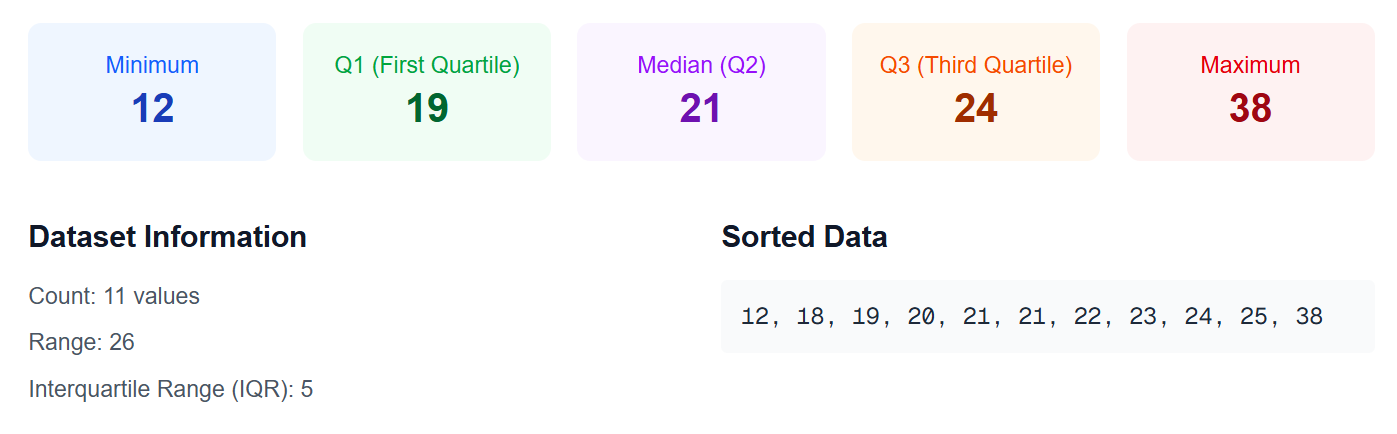
Dataset 3: Daily Temperature Records (°C)

22, 23, 21, 25, 24, 20, 19, 18, 21, 12, 38
  • Minimum: 12
  • Q1: 19
  • Median (Q2): 21
  • Q3: 24
  • Maximum: 38
Normal temperatures are between 18°C and 25°C, but there are extreme low (12°C) and high (38°C) values.
Five number summary box plot for daily temperature records

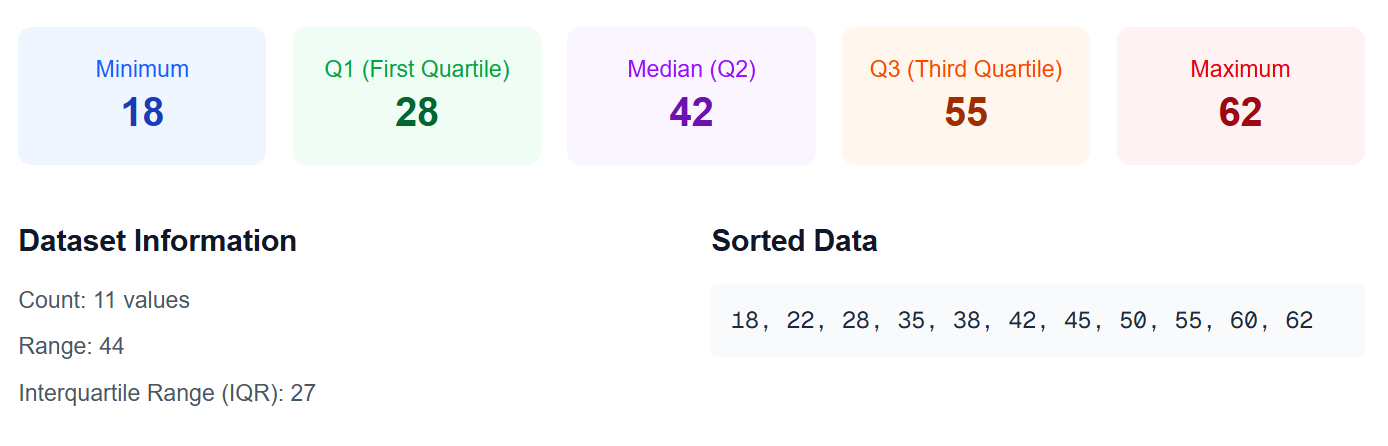
Dataset 4: City PM2.5 Index

45, 38, 42, 50, 55, 60, 62, 35, 28, 22, 18
  • Minimum: 18
  • Q1: 28
  • Median (Q2): 42
  • Q3: 55
  • Maximum: 62
Most days have moderate pollution, but a few days show exceptionally good air quality.
Five number summary box plot for city PM2.5 index

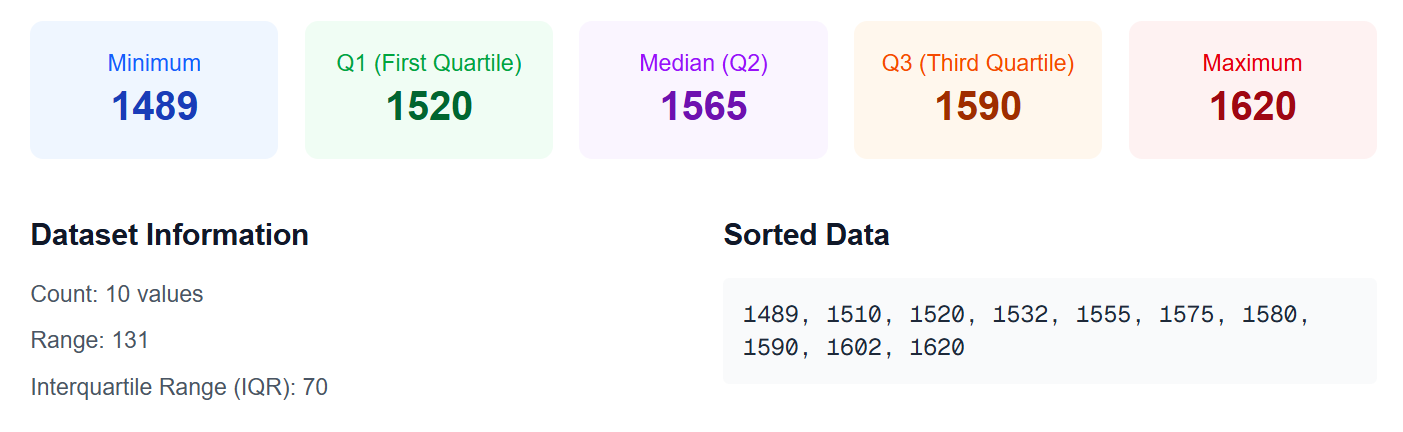
Dataset 5: Daily Active Users of an App

1532, 1489, 1620, 1555, 1580, 1602, 1520, 1575, 1590, 1510
  • Minimum: 1489
  • Q1: 1520
  • Median (Q2): 1565
  • Q3: 1590
  • Maximum: 1620
User count is stable between 1500 and 1600, with only minor fluctuations.
Five number summary box plot for daily active users of an app